A variation of a puzzle called the “pick-up sticks problem” asks the following question: If I have some number of sticks with random lengths between 0 and 1, what are the chances that no three of those sticks can form a triangle? It turns out the answer to this quandary has an unexpected parallel to a pattern found across nature.
The Fibonacci sequence is an ordered collection of numbers in which each term is equal to the previous two added together. It goes like this: 1, 1, 2, 3, 5, 8, 13,…, and so on. These numbers show up practically everywhere. If you look at a plant with spirals, such as a pine cone or pineapple, more likely than not, the number of spirals going in each direction will be consecutive terms of the Fibonacci sequence. But a pair of young researchers were surprised to find that this pattern and the pick-up sticks problem are deeply connected.
On supporting science journalism
If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
The pick-up sticks problem is a variant of the “broken stick problem,” which can be traced back to at least 1854. In its simplest iteration, the broken stick problem asks the likelihood that a stick broken randomly into three pieces can form a triangle. (In the pick-up stick problem, the lengths don’t need to add up to a particular whole, so the possible lengths are distributed differently.) More than a century later, in the October 1959 issue of Scientific American, Martin Gardner wrote about the broken stick problem for his Mathematical Games column. Gardner highlighted it as a classic example of the counterintuitive nature of problems in probability and statistics. In a preprint paper posted to the server arXiv.org in May, the young researchers and their collaborators explore a new variation of the pick-up sticks problem.
This effort started when Arthur Sun, a first-year undergraduate student at the University of Cambridge, thought up a problem for a university math contest. What is the likelihood, he wondered, that out of four sticks with random lengths between 0 and 1, no three could make a triangle? He enlisted the help of his friend Edward Wang, at the time a 12th grader at Scotch College, a secondary school in Australia, where he and Sun originally met. Together, Wang and Sun modeled the problem on their computers and ran random trials over and over, keeping track of the results of each trial. It seemed to the pair that four sticks could not make a triangle among them very close to one sixth of the time.
Soon Wang and Sun started wondering what the answer was for larger groupings of sticks. They enlisted the help of David Treeby, a mathematician affiliated with Australia’s Monash University and a teacher at Scotch College. The group ran even more simulations, and soon a pattern started to emerge.
According to the researchers’ simulations, if n was the number of sticks selected randomly, the chance of not having a valid triangle among them was the reciprocal of the first n Fibonacci numbers multiplied together. For instance, if you pick six sticks randomly, the probability that you cannot make a triangle with them is 1 / (1 × 1 × 2 × 3 × 5 × 8) = 1⁄240. The team was surprised that the famous sequence was connected to the triangle problem. “We’d no reason to suspect that it would be,” Treeby says, “but it was impossible that it wasn’t.”
The researchers began to develop a proof of why this connection must be true, but they needed an expert in statistics to pull it all together. They brought in a fourth collaborator, former Monash mathematician Aidan Sudbury. He’d been happily enjoying his retirement when the team approached him.
“I immediately was struck by what a charming problem it was,” he says. “Delightful!” Together, the four researchers worked out a solid proof of the pattern that Sun and Wang had noticed. Though related results have been proved using similar methods and encompassing a wide array of stick-and-triangle problems, some experts in the field find this new paper’s simplicity refreshing. “What’s nice about this is: it’s very well written,” says Steven Miller, a mathematician at Williams College and president of the Fibonacci Association. “It’s accessible, it’s easy to read, and it’s extending a very famous problem.”
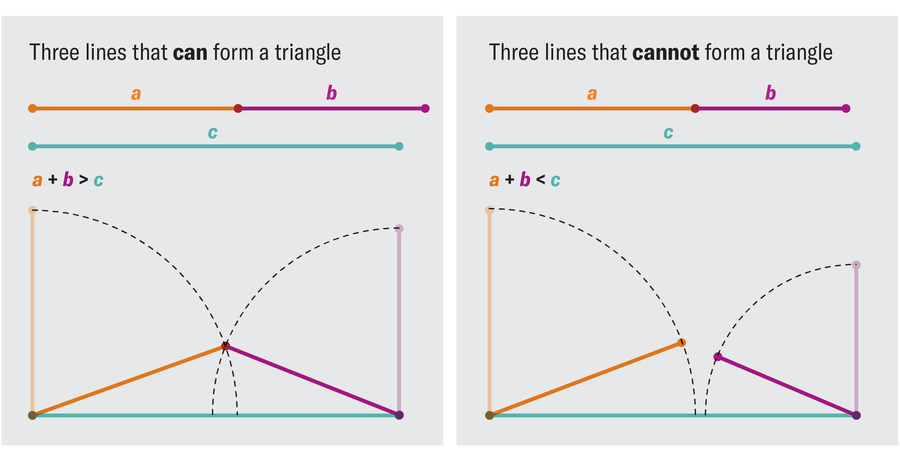
To understand the pick-up sticks solution, think about the smallest possible case. Suppose you have three sticks with random sizes between 0 and 1. Any three sticks can form a triangle if, and only if, no stick is longer than the other two put together. If you have sticks of lengths 1, 2 and 300, no matter how wide an angle you put between them, the first two sticks could never stretch wide enough to accommodate the third. This is called “the triangle inequality”: if a, b and c represent the lengths of the sticks from shortest to longest, they will only fail to form a triangle when a + b ≤ c.
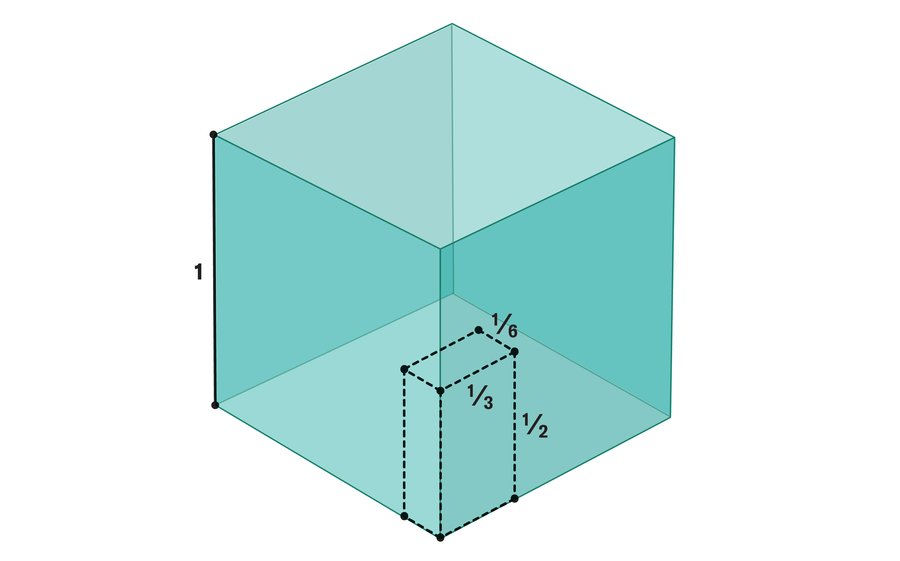
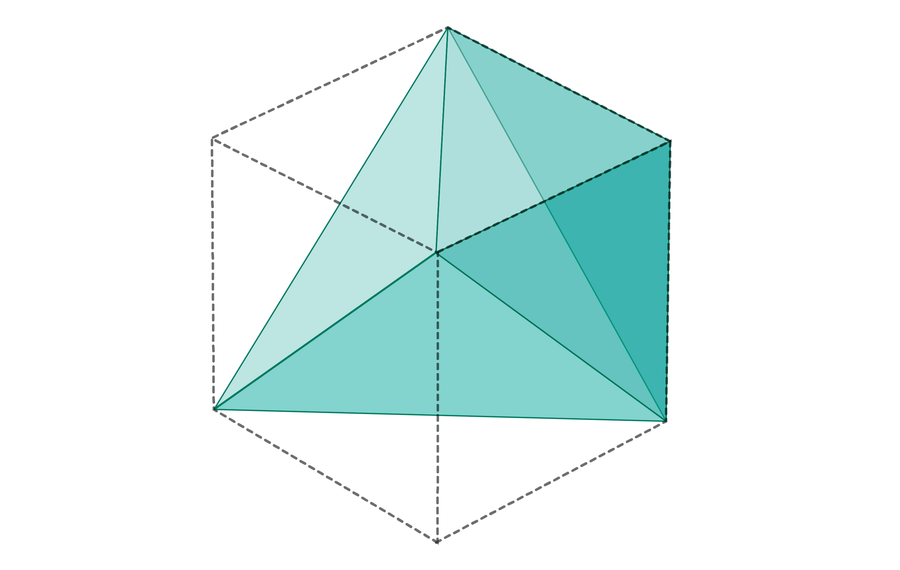
To find the probability that three random lengths form a triangle, mathematicians can consider every set of three lengths as a point in three-dimensional space (for instance, lengths 1⁄2, 1⁄6 and 1⁄3 are represented by the point [1⁄2, 1⁄6,1⁄3]). Because the lengths fall between 0 and 1, the set of all such points can be represented by a unit cube:
Researchers then look at the subset of this cube where the points satisfy the triangle inequality—a shape that looks like this:
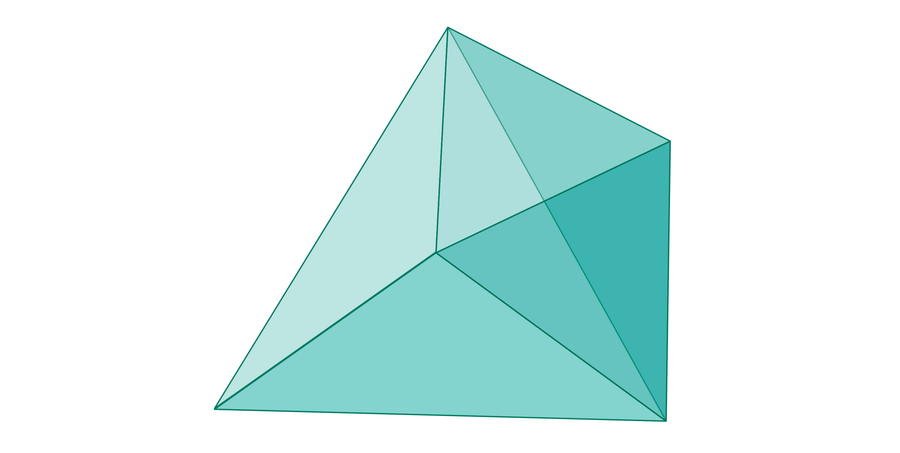
With a little geometry, it turns out that this shape is exactly half the volume of the cube. Thus, three randomly picked lengths will be able to form a triangle exactly half of the time, as 1 / (1 × 1 × 2) = 1⁄2.
Where does Fibonacci come in? Suppose a collection of any number of sticks is ordered from shortest to longest. If no three among them form a triangle, each stick’s length must be greater than or equal to the sum of the previous two—otherwise, those three sticks could make a triangle. In the Fibonacci sequence, each number is precisely equal to the sum of the previous two. In other words, each segment of the Fibonacci sequence is as close as possible to having a triangle in it without actually having one. In Treeby’s words, “If we [avoid triangles] greedily, the Fibonacci sequence appears naturally.”
The researchers feel there should be some path directly from this insight to a proof of the pick-up sticks theorem. They couldn’t find one, however. “We sort of hoped to find something that was a little bit more … intuitive, but we couldn’t formalize our thinking,” Treeby says. Instead their paper uses integrals to calculate the high-dimensional volumes directly—a method a bit like looking at the area inside the cube above (but without the visual reference). The researchers aren’t on the prowl for a different proof right now—but they hope someone else might find one.
It’s Time to Stand Up for Science
Before you close the page, we need to ask for your support. Scientific American has served as an advocate for science and industry for 180 years, and we think right now is the most critical moment in that two-century history.
We’re not asking for charity. If you become a Digital, Print or Unlimited subscriber to Scientific American, you can help ensure that our coverage is centered on meaningful research and discovery; that we have the resources to report on the decisions that threaten labs across the U.S.; and that we support both future and working scientists at a time when the value of science itself often goes unrecognized. Click here to subscribe.




